
2022年06月28日

导语
本文介绍AES和SM4 S盒的复合域实现方法,该方法由D.Canright在《A Very Compact Rijndael S-box》一文中提出,是分组密码bitslice实现、受限资源算法硬件实现和一些掩码方案的基础。
1背景
是的,你没看错。本文要讲一下如何实现 AES 和 SM4 的 S 盒实现。你可能好奇,S 盒实现有什么好讲的,c 语言一个unsigned int Sbox[256] = {...},verilog 一个always case xxx:解决问题。没错,查表实现是S盒最基本的实现方法。高端一点的查表,可以将 S 盒的实现结合线性变换(AES 的 MixColumn,SM4 的 L)形成8→32的大表 T-Table 进行加速,例如openssl的查表实现。
其实,我们本文将探讨一种不通过查表,只是通过逻辑运算的 S 盒实现方法。
AES 和 SM4 的 S 盒都是由 GF(28) 有限域上的运算进行生成的。我们可以直接基于其实现方法,对 S 盒进行计算实现。在 AES 和 SM4 的 S 盒生成公式中,均设计在 GF(28) 的求逆运算,该运算比较耗时。有限域中求逆运算可以转化幂运算,例如 AES 的 S 盒可以表达为:
S(x)=63+05x254+09x253+F9x251+25x247+01x223+B5x191+8Fx127.
该运算定义在GF(28)上,直接实现同样较为复杂。
还有一种方法,是使用布尔函数对 S 盒进行表达,利用布尔函数进行实现。该方法其实可以看作GF(2)上的表达。On Deviations of the AES S-box when Represented as Vector Valued Boolean Function对 AES 的 S 盒进行了分析,得到其布尔函数表达式,例如,其中第0比特可表示为:
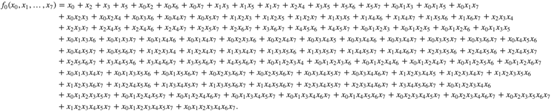
布尔函数非常复杂,直接利用布尔函数表达式也不是一个好的思路。
D.Canright在A Very Compact Rijndael S-box一文中,提出一种实现思路:基于复合域进行实现。文章提出该方法实现在资源有限情况下的该类 S 盒的实现方式,后该方法被用于构造掩码实现(抵抗DPA攻击)和bitslice实现上。本文将对这个方法进行介绍。
2原理
AES 和 SM4 的 S 盒生成都是基于GF(28)进行构造的,利用逆运算和仿射变换(affine)。仿射变换本身就能表示成逻辑运算,我们重点关注求逆运算。AES 和 SM4 的表达都是基于多项式基,以 AES 的有限域为例,假设A为多项式x8+x4+x3+x+1的根,即A8+A4+A3+A+1=0。那么任何一个元素x可以表示为x=x7A7+x6A6+x5A5+x4A4+x3A3+x2A2+x1A+x0。这种做法是将GF(28)直接看作GF(2)的8次扩域。我们也可以不这么看,将GF(28)看成GF(24)的2次扩域,GF(24)可以进一步看作GF(22)的2次扩域,再进一步GF(22)可以看作GF(2)的2次扩域。而GF(28)的求逆运算,可以通过数学表达式,转换为GF(24)的求逆和一些乘、加操作。这些操作可以进一步向下转化。下面我们详细说明一下。
K=GF(qn)为GF(q)的n次扩域,β 为多项式的根,那么多项式基为{1,β,β2,…,βn−1},任何一个元素x,可以表示为x=xn−1βn−1+…+x1β+x0,这也是AES 和 SM4 所采用的基表示方式。此外,除了多项式基以外,域的表达方式还可以使用正规基进行表达,正规基为{β,βq,βq2,…,βqn−1},正规基使用了多项式的全部根。
GF(28),可以看作GF(24)的2次扩域,也就是在GF(24)上寻找一个不可约二次多项式,r(y)=y2+τy+υ,其中,τ 和 υ 为 GF(24) 的元素。设 Y 为 r(y) 的根,则 GF(28) 元素的多项式基为 Y,1,正规基为Y,Y16。Canright在文章中讨论了多项式基和正规基两种方式,我们这里只看正规基。对于GF(28)的元素 g=γ1Y16+γ0Y,求逆 d=δ1Y16+δ0Y,γi 和 δi 都是GF(24)的元素, gd=1,待定系数求解,可得出
{
δ1=[γ1γ0τ2+(γ21+γ20)υ]−1γ0δ0=[γ1γ0τ2+(γ21+γ20)υ]−1γ1
文内有详细推导方法,不再赘述。观察系数,其达到的效果就是,GF(28)的求逆运算,转化成为GF(24)的乘法、平方和求逆,特别的,可以选择不可约多项式为r(y)=y2+y+υ,也就是 τ 取1来降低求解复杂度,这样,对g=γ1Y16+γ0Y的求逆可简化为如下图:
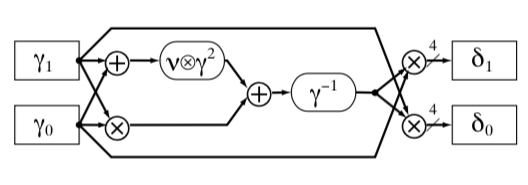
同样,GF(24)可以看作GF(22)的二次扩域,也就是在GF(22)寻找一个不可约二次多项式,s(z)=z2+Tz+N,设Z 为该多项式的根,取正规基{Z4,Z}。和GF(28)计算方法相同,可计算GF(24)元素υ=Γ1Z4+Γ0Z 的逆为δ=ΔZ4+ΔZ,其中,
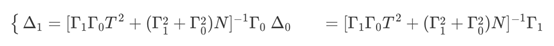
也可以取T=1降低复杂度,那么在GF(24)求逆运算如下图所示:
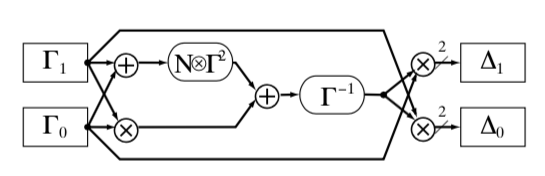
在GF(28)求逆时,也涉及到了GF(24)的乘法。GF(24)的乘法υδ=(Γ1Z4+Γ0Z)(Δ1Z4+Δ0Z)可按照如下公式计算:

如下图:
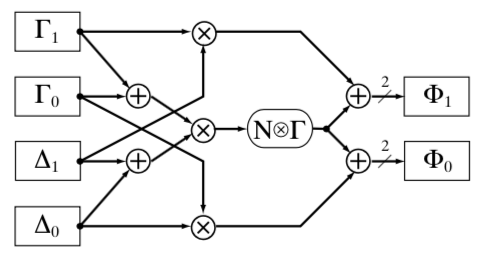
进一步,GF(22)可以看作GF(2)的二次扩域,在GF(2)上的不可约多项式只有t(ω)=ω2+ω+1,取正规基W2,W,则Γ=g1W2+g0W,逆为Δ=d1W2+d0W,其中,
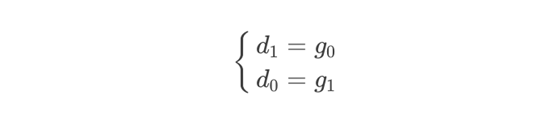
GF(22)的乘法,ΓΔ=(g1W2+g0W)(d1W2+d0W),计算如下:
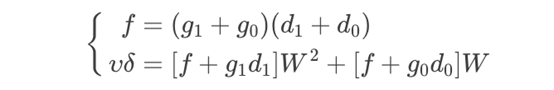
如下图:
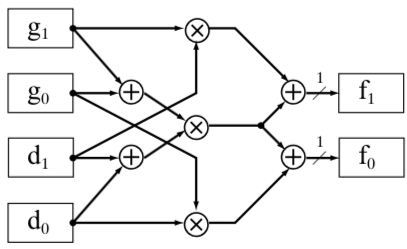
将GF(28)进行转化,我们还有一些操作未介绍,包括 υγ2、NΓ2 和 NΓ。这些值可通过选择不同的 υ 和 N 进行简化。文章详细讨论了选取的方法。我们直接给结论:
对于GF(22),不可约多项式为t(ω)=ω2+ω+1,正规基{W2,W}
对于GF(24)/GF(22),不可约多项式为s(z)=z2+z+N,N=W2,正规基Z4,Z,N(g1W2+g2W)2=W2(g1W2+g2W)=g1W2+(g1+g0)W
对于GF(28)/GF(24),不可约多项式为r(y)=y2+y+υ,υ=N2Z,如此,υ(AZ4+BZ)2=(A+B)2Z4+N2B2
复合域下,实际上是以
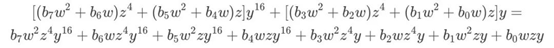
表示GF(28)的一个元素。
而 S 盒的输入是以多项式基表示进行输入的。要利用复合域进行运算,需要将输入表示进行转换。以线性空间的角度看,这复合域表示相当于是给GF(28)找了一组新基。两组基有如下关系:
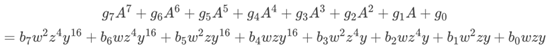
找到w2z4y16等在多项式基下的表示,形成矩阵X:
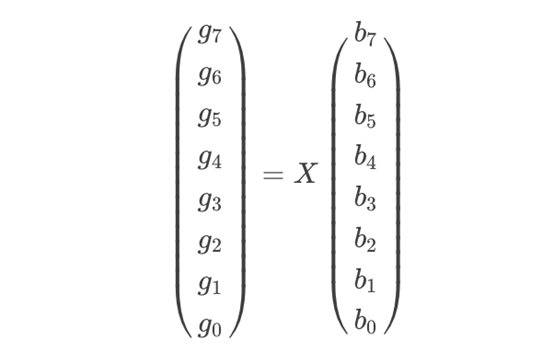
计算X−1,乘以多项式基下的表示即可得到复合域基下的表示。S盒计算完成后,再进行反变换即可。
3AES S盒实现方法
AES的S盒是定义在GF(28)(不可约多项式x8+x4+x3+x+1),其表达式为S(x)=Ax−1+c,具体如下:

4求矩阵X和逆
求 X 和 X−1,我们需要计算 w,z 和 y,计算 w2z4y16等一系列系数值。Canright在文章中给出了 GF(28) 生成元 B 的 对数表,方便计算。这里我们直接通过搜索进行计算。
from pyfinite import ffield
gen = 0b100011011
F = ffield.FField(8, gen, useLUT=0) # 这里一定要写useLUT=0,不然会出问题。。。
def field_pow2(x, F): #计算在F域上的平方
return F.Multiply(x, x)
def field_pow3(x, F): #计算在F域上的三次方
return F.Multiply(x, field_pow2(x, F))
def field_pow4(x, F): #计算在F域上的四次方
return field_pow2(field_pow2(x, F), F)
首先,搜索GF(22)的正规基{W2,W},我们求出其在GF(28)下多项式基的表示。
for i in range(256):
if field_pow2(i, F)^i^1 == 0: # 搜索 w^2+w+1 = 0的根
print(hex(i))
我们可得到,W=0xbd,W2=0xbc(一定要注意,这是GF(28)的多项式基表示)
2. 然后,搜索GF(24)/GF(22)的正规基Z4,Z,我们求出其在GF(28)下多项式基的表示。s(z)=z2+z+N,N=W2=0xbc
for i in range(256):
if field_pow2(i, F)^i^0xbc == 0: # 搜索 z^2+z+0xbc = 0的根
print(hex(i))
于是我们又得到,Z=0x5c,Z4=0x5d
3. 最后,搜索GF(28)/GF(24)的正规基{Y16,Y},我们求出其在GF(28)下多项式基的表示。r(y)=y2+y+υ,υ=N2Z
u = F.Multiply(field_pow2(0xbc, F), 0x5c)
for i in range(256):
if field_pow2(i, F)^i^0xec == 0: # 搜索 z^2+z+0xbc = 0的根
print(hex(i))
于是我们又得到,Y=0xff,Y16=0xfe
w = 0xbd
w_2 = 0xbc
z = 0x5c
z_4 = 0x5d
y = 0xff
y_16 = 0xfe
w_2_z_4_y_16 = F.Multiply(F.Multiply(w_2, z_4), y_16)
w_z_4_y_16 = F.Multiply(F.Multiply(w, z_4), y_16)
w_2_z_y_16 = F.Multiply(F.Multiply(w_2, z), y_16)
w_z_y_16 = F.Multiply(F.Multiply(w, z), y_16)
w_2_z_4_y = F.Multiply(F.Multiply(w_2, z_4), y)
w_z_4_y = F.Multiply(F.Multiply(w, z_4), y)
w_2_z_y = F.Multiply(F.Multiply(w_2, z), y)
w_z_y = F.Multiply(F.Multiply(w, z), y)
print('w_2_z_4_y_16\t', hex(w_2_z_4_y_16))
print('w_z_4_y_16\t', hex(w_z_4_y_16))
print('w_2_z_y_16\t', hex(w_2_z_y_16))
print('w_z_y_16\t', hex(w_z_y_16))
print('w_2_z_4_y\t', hex(w_2_z_4_y))
print('w_z_4_y\t\t', hex(w_z_4_y))
print('w_2_z_y\t\t', hex(w_2_z_y))
print('w_z_y\t\t', hex(w_z_y))
得到多项式基在复合域基下表示如下:

求X−1,可得到复合域基下多项式基的表示:
from pyfinite import genericmatrix
XOR = lambda x,y: x^y
AND = lambda x,y: x&y
DIV = lambda x,y: x
m = genericmatrix.GenericMatrix(size=(8, 8),zeroElement=0,identityElement=1,add=XOR,mul=AND,sub=XOR,div=DIV)
m.SetRow(0, [0, 0, 0, 1, 0, 0, 1, 0])
m.SetRow(1, [1, 1, 1, 0, 1, 0, 1, 1])
m.SetRow(2, [1, 1, 1, 0, 1, 1, 0, 1])
m.SetRow(3, [0, 1, 0, 0, 0, 0, 1, 0])
m.SetRow(4, [0, 1, 1, 1, 1, 1, 1, 0])
m.SetRow(5, [1, 0, 1, 1, 0, 0, 1, 0])
m.SetRow(6, [0, 0, 1, 0, 0, 0, 1, 0])
m.SetRow(7, [0, 0, 0, 0, 0, 1, 0, 0])
print(m)
print(m.Inverse())

5具体函数实现
基础函数定义
g2b = [0b10011000, 0b11110011, 0b11110010, 0b01001000, 0b00001001, 0b10000001, 0b10101001, 0b11111111]
b2g = [0b01100100, 0b01111000, 0b01101110, 0b10001100, 0b01101000, 0b00101001, 0b11011110, 0b01100000]
def G4_mul(x, y):
'''
GF(2^2)的乘法运算,正规基{W^2, W}
'''
a = (x & 0x02)>>1
b = x & 0x01
c = (y & 0x02)>>1
d = y & 0x01
e = (a ^ b) & (c ^ d)
return (((a & c) ^ e) << 1)|((b & d) ^ e)
def G4_mul_N(x):
'''
GF(2^2)的乘N操作,N = W^2
'''
a = (x & 0x02)>>1
b = x & 0x01
p = b
q = a ^ b
return (p<<1)|q
def G4_mul_N2(x):
'''
GF(2^2)的乘N^2操作,N = W^2
'''
a = (x & 0x02)>>1
b = x & 0x01
return ((a ^ b)<<1)|a
def G4_inv(x):
'''
GF(2^2)的求逆操作,该操作和GF(2^2)的平方操作等价
'''
a = (x & 0x02)>>1
b = x & 0x01
return (b<<1)|a
def G16_mul(x, y):
'''
GF(2^4)的乘法操作,正规基{Z^4, Z}
'''
a = (x & 0xc)>>2
b = x & 0x03
c = (y & 0xc)>>2
d = y & 0x03
e = G4_mul(a ^ b, c ^ d)
e = G4_mul_N(e)
p = G4_mul(a, c) ^ e
q = G4_mul(b, d) ^ e
return (p<<2) | q
def G16_sq_mul_u(x):
'''
GF(2^4)的平方后乘u操作, u = N^2Z, N = W^2
'''
a = (x & 0xc)>>2
b = x & 0x03
p = G4_inv(a ^ b) # G4平方和求逆等价
q = G4_mul_N2(G4_inv(b))
return (p<<2)|q
def G16_inv(x):
'''
GF(2^4)的求逆操作
'''
a = (x & 0xc)>>2
b = x & 0x03
c = G4_mul_N(G4_inv(a ^ b))
d = G4_mul(a, b)
e = G4_inv(c ^ d)
p = G4_mul(e, b)
q = G4_mul(e, a)
return (p<<2)|q
def G256_inv(x):
'''
GF(2^8)的求逆操作
'''
a = (x & 0xF0)>>4
b = x & 0x0F
c = G16_sq_mul_u(a ^ b)
d = G16_mul(a, b)
e = G16_inv(c ^ d)
p = G16_mul(e, b)
q = G16_mul(e, a)
return (p<<4)|q
def G256_new_basis(x, b):
'''
x在新基b下的表示
'''
y = 0
for i in range(8):
if x & (1<<(7-i)):
y ^= b[i]
return y
计算S盒输出值
A = [0b10001111, 0b11000111, 0b11100011, 0b11110001, 0b11111000, 0b01111100, 0b00111110, 0b00011111] #仿射变换矩阵乘
def AES_SBOX(x):
t = G256_new_basis(x, g2b)
t = G256_inv(t)
t = G256_new_basis(t, b2g)
t = G256_new_basis(t, A) #仿射变换乘
return t ^ 0x63
sbox = []
for i in range(256):
sbox.append(AES_SBOX(i)) # 生成sbox
for i,s in enumerate(sbox):
print(f'%02x'%s,', ', end='')
if (i+1)%16==0:
print()
6SM4 S盒实现方法
SM4 的 S 盒和 AES 不同, 定义在GF(28)采用的不可约多项式为x8+x7+x6+x5+x4+x2+1,生成方式为S(x)=A(Ax+c)−1+c,其中:

7求矩阵X和逆
不可约多项式不同,X 矩阵也不相同。下面我们为 SM4 求 X 和 X−1,我们需要计算 w,z 和 y,计算 w2z4y16等一系列系数值
from pyfinite import ffield
gen = 0b111110101
F = ffield.FField(8, gen, useLUT=0) # 这里一定要写useLUT=0,不然会出问题。。。
首先,搜索GF(22)的正规基{W2,W},我们求出其在GF(28)下多项式基的表示。
for i in range(256):
if field_pow2(i, F)^i^1 == 0: # 搜索 w^2+w+1 = 0的根
print(hex(i))
我们得到,W=0x5d,W2=0x5c(一定要注意,这是GF(28)的多项式基表示)
然后,搜索GF(24)/GF(22)的正规基Z4,Z,我们求出其在GF(28)下多项式基的表示。s(z)=z2+z+N,N=W2=0x5c
for i in range(256):
if field_pow2(i, F)^i^0x5c == 0: # 搜索 z^2+z+0x5c = 0的根
print(hex(i))
于是我们又得到,Z=0x0c,Z4=0x0d
最后,搜索GF(28)/GF(24)的正规基Y16,Y,我们求出其在GF(28)下多项式基的表示。r(y)=y2+y+υ,υ=N2Z
u = F.Multiply(field_pow2(0x5c, F), 0x0c)
for i in range(256):
if field_pow2(i, F)^i^0x76 == 0: # 搜索 z^2+z+0x76 = 0的根
print(hex(i))
于是我们又得到,Y=0xef,Y16=0xee
w = 0x5d
w_2 = 0x5c
z = 0x0c
z_4 = 0x0d
y = 0xef
y_16 = 0xee
w_2_z_4_y_16 = F.Multiply(F.Multiply(w_2, z_4), y_16)
w_z_4_y_16 = F.Multiply(F.Multiply(w, z_4), y_16)
w_2_z_y_16 = F.Multiply(F.Multiply(w_2, z), y_16)
w_z_y_16 = F.Multiply(F.Multiply(w, z), y_16)
w_2_z_4_y = F.Multiply(F.Multiply(w_2, z_4), y)
w_z_4_y = F.Multiply(F.Multiply(w, z_4), y)
w_2_z_y = F.Multiply(F.Multiply(w_2, z), y)
w_z_y = F.Multiply(F.Multiply(w, z), y)
print('w_2_z_4_y_16\t', hex(w_2_z_4_y_16))
print('w_z_4_y_16\t', hex(w_z_4_y_16))
print('w_2_z_y_16\t', hex(w_2_z_y_16))
print('w_z_y_16\t', hex(w_z_y_16))
print('w_2_z_4_y\t', hex(w_2_z_4_y))
print('w_z_4_y\t\t', hex(w_z_4_y))
print('w_2_z_y\t\t', hex(w_2_z_y))
print('w_z_y\t\t', hex(w_z_y))
得到多项式基在复合域基下表示如下:

求X−1,可得到复合域基下多项式基的表示:
from pyfinite import genericmatrix
XOR = lambda x,y: x^y
AND = lambda x,y: x&y
DIV = lambda x,y: x
m = genericmatrix.GenericMatrix(size=(8, 8),zeroElement=0,identityElement=1,add=XOR,mul=AND,sub=XOR,div=DIV)
m.SetRow(0, [1, 1, 0, 1, 1, 1, 0, 1])
m.SetRow(1, [1, 1, 1, 0, 1, 1, 0, 1])
m.SetRow(2, [1, 1, 0, 1, 0, 0, 1, 0])
m.SetRow(3, [1, 0, 1, 0, 1, 0, 0, 1])
m.SetRow(4, [0, 1, 0, 0, 0, 0, 1, 0])
m.SetRow(5, [1, 1, 1, 0, 0, 1, 1, 1])
m.SetRow(6, [0, 0, 0, 1, 1, 1, 1, 0])
m.SetRow(7, [0, 0, 0, 0, 0, 1, 0, 0])
print(m)
print(m.Inverse())
8具体函数实现
基础函数定义
SM4 和 AES 采用的复合域结构相同,其基础函数也相同。仅定义X矩阵即可。
g2b = [0b00100001, 0b11010011, 0b10000001, 0b01001010, 0b10001010, 0b10111001, 0b10110000, 0b11111111]
b2g = [0xf4, 0xec, 0x54, 0xa2, 0xd2, 0xc7, 0x2e, 0xd4]
A = [0b11100101, 0b11110010, 0b01111001, 0b10111100, 0b01011110, 0b00101111, 0b10010111, 0b11001011]
def SM4_SBOX(x):
t = G256_new_basis(x, A)
t ^= 0xd3
t = G256_new_basis(t, g2b)
t = G256_inv(t)
t = G256_new_basis(t, b2g)
t = G256_new_basis(t, A) #仿射变换乘
return t ^ 0xd3
sbox = []
for i in range(256):
sbox.append(SM4_SBOX(i)) # 生成sbox
for i,s in enumerate(sbox):
print(f'%02x'%s,', ', end='')
if (i+1)%16==0:
print()
9推广结论
通过 AES 和 SM4 的 S 盒复合域实现,我们不难发现,在复合域上,AES 和 SM4 的求逆运算过程相同,而除此之外,其他操作都是线性的仿射变换。那么我们能不能通过 AES 的 S 盒计算 SM4 的 S 盒输出呢?也就是,
Ssm4(x)=L(Saes(Mx+C1))+C2,下面我们尝试进行推导。
假设复合域求逆运算为f,则
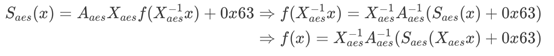
由此得出:
Ssm4(x)=Asm4Xsm4f(X−1sm4(Asm4x+0xd3))+0xd3⇒Ssm4(x)=Asm4Xsm4X−1aesA−1aes(Saes(Xaes(X−1sm4(Asm4x+0xd3)))+0x63)+0xd3
由此可得出,
XOR = lambda x,y: x^y
AND = lambda x,y: x&y
DIV = lambda x,y: x
X_aes = genericmatrix.GenericMatrix(size=(8, 8),zeroElement=0,identityElement=1,add=XOR,mul=AND,sub=XOR,div=DIV)
X_sm4 = genericmatrix.GenericMatrix(size=(8, 8),zeroElement=0,identityElement=1,add=XOR,mul=AND,sub=XOR,div=DIV)
A_aes = genericmatrix.GenericMatrix(size=(8, 8),zeroElement=0,identityElement=1,add=XOR,mul=AND,sub=XOR,div=DIV)
A_sm4 = genericmatrix.GenericMatrix(size=(8, 8),zeroElement=0,identityElement=1,add=XOR,mul=AND,sub=XOR,div=DIV)
c_aes = genericmatrix.GenericMatrix(size=(8, 1),zeroElement=0,identityElement=1,add=XOR,mul=AND,sub=XOR,div=DIV)
c_sm4 = genericmatrix.GenericMatrix(size=(8, 1),zeroElement=0,identityElement=1,add=XOR,mul=AND,sub=XOR,div=DIV)
X_aes.SetRow(0, [0, 0, 0, 1, 0, 0, 1, 0])
X_aes.SetRow(1, [1, 1, 1, 0, 1, 0, 1, 1])
X_aes.SetRow(2, [1, 1, 1, 0, 1, 1, 0, 1])
X_aes.SetRow(3, [0, 1, 0, 0, 0, 0, 1, 0])
X_aes.SetRow(4, [0, 1, 1, 1, 1, 1, 1, 0])
X_aes.SetRow(5, [1, 0, 1, 1, 0, 0, 1, 0])
X_aes.SetRow(6, [0, 0, 1, 0, 0, 0, 1, 0])
X_aes.SetRow(7, [0, 0, 0, 0, 0, 1, 0, 0])
print(X_aes)
X_aes_inv = X_aes.Inverse()
X_aes_inv
X_sm4.SetRow(0, [1, 1, 0, 1, 1, 1, 0, 1])
X_sm4.SetRow(1, [1, 1, 1, 0, 1, 1, 0, 1])
X_sm4.SetRow(2, [1, 1, 0, 1, 0, 0, 1, 0])
X_sm4.SetRow(3, [1, 0, 1, 0, 1, 0, 0, 1])
X_sm4.SetRow(4, [0, 1, 0, 0, 0, 0, 1, 0])
X_sm4.SetRow(5, [1, 1, 1, 0, 0, 1, 1, 1])
X_sm4.SetRow(6, [0, 0, 0, 1, 1, 1, 1, 0])
X_sm4.SetRow(7, [0, 0, 0, 0, 0, 1, 0, 0])
print(X_sm4)
X_sm4_inv = X_sm4.Inverse()
X_sm4_inv
A_aes.SetRow(0, [1, 1, 1, 1, 1, 0, 0, 0])
A_aes.SetRow(1, [0, 1, 1, 1, 1, 1, 0, 0])
A_aes.SetRow(2, [0, 0, 1, 1, 1, 1, 1, 0])
A_aes.SetRow(3, [0, 0, 0, 1, 1, 1, 1, 1])
A_aes.SetRow(4, [1, 0, 0, 0, 1, 1, 1, 1])
A_aes.SetRow(5, [1, 1, 0, 0, 0, 1, 1, 1])
A_aes.SetRow(6, [1, 1, 1, 0, 0, 0, 1, 1])
A_aes.SetRow(7, [1, 1, 1, 1, 0, 0, 0, 1])
print(A_aes)
A_aes_inv = A_aes.Inverse()
A_sm4.SetRow(0, [1, 1, 0, 1, 0, 0, 1, 1])
A_sm4.SetRow(1, [1, 1, 1, 0, 1, 0, 0, 1])
A_sm4.SetRow(2, [1, 1, 1, 1, 0, 1, 0, 0])
A_sm4.SetRow(3, [0, 1, 1, 1, 1, 0, 1, 0])
A_sm4.SetRow(4, [0, 0, 1, 1, 1, 1, 0, 1])
A_sm4.SetRow(5, [1, 0, 0, 1, 1, 1, 1, 0])
A_sm4.SetRow(6, [0, 1, 0, 0, 1, 1, 1, 1])
A_sm4.SetRow(7, [1, 0, 1, 0, 0, 1, 1, 1])
print(A_sm4)
A_sm4_inv = A_sm4.Inverse()
M = X_aes*X_sm4_inv*A_sm4
print(M)
A = [0, 1, 1, 0, 0, 0, 1, 1]
for i in range(8):
c_aes.SetRow(i, [A[i]])
print(c_aes)
A = [1, 1, 0, 1, 0, 0, 1, 1]
for i in range(8):
c_sm4.SetRow(i, [A[i]])
print(c_sm4)
C1 = X_aes*(X_sm4_inv*c_sm4)
print(C1)
L = A_sm4*X_sm4*X_aes_inv*A_aes_inv
print(L)
因此,
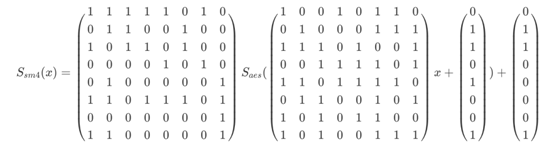
可以进行程序验证如下:
L = [0b10100101, 0b11001101, 0b11100000, 0b10100100, 0b10010100, 0b01100100, 0b10010000, 0b00001111]
M = [0b10101011, 0b01101100, 0b00110111, 0b10011000, 0b00111010, 0b11011111, 0b11001001, 0b01110101]
c1 = 0x69
c2 = 0x61
SBOX_AES = [0x63 , 0x7c , 0x77 , 0x7b , 0xf2 , 0x6b , 0x6f , 0xc5 , 0x30 , 0x01 , 0x67 , 0x2b , 0xfe , 0xd7 , 0xab , 0x76 ,
0xca , 0x82 , 0xc9 , 0x7d , 0xfa , 0x59 , 0x47 , 0xf0 , 0xad , 0xd4 , 0xa2 , 0xaf , 0x9c , 0xa4 , 0x72 , 0xc0 ,
0xb7 , 0xfd , 0x93 , 0x26 , 0x36 , 0x3f , 0xf7 , 0xcc , 0x34 , 0xa5 , 0xe5 , 0xf1 , 0x71 , 0xd8 , 0x31 , 0x15 ,
0x04 , 0xc7 , 0x23 , 0xc3 , 0x18 , 0x96 , 0x05 , 0x9a , 0x07 , 0x12 , 0x80 , 0xe2 , 0xeb , 0x27 , 0xb2 , 0x75 ,
0x09 , 0x83 , 0x2c , 0x1a , 0x1b , 0x6e , 0x5a , 0xa0 , 0x52 , 0x3b , 0xd6 , 0xb3 , 0x29 , 0xe3 , 0x2f , 0x84 ,
0x53 , 0xd1 , 0x00 , 0xed , 0x20 , 0xfc , 0xb1 , 0x5b , 0x6a , 0xcb , 0xbe , 0x39 , 0x4a , 0x4c , 0x58 , 0xcf ,
0xd0 , 0xef , 0xaa , 0xfb , 0x43 , 0x4d , 0x33 , 0x85 , 0x45 , 0xf9 , 0x02 , 0x7f , 0x50 , 0x3c , 0x9f , 0xa8 ,
0x51 , 0xa3 , 0x40 , 0x8f , 0x92 , 0x9d , 0x38 , 0xf5 , 0xbc , 0xb6 , 0xda , 0x21 , 0x10 , 0xff , 0xf3 , 0xd2 ,
0xcd , 0x0c , 0x13 , 0xec , 0x5f , 0x97 , 0x44 , 0x17 , 0xc4 , 0xa7 , 0x7e , 0x3d , 0x64 , 0x5d , 0x19 , 0x73 ,
0x60 , 0x81 , 0x4f , 0xdc , 0x22 , 0x2a , 0x90 , 0x88 , 0x46 , 0xee , 0xb8 , 0x14 , 0xde , 0x5e , 0x0b , 0xdb ,
0xe0 , 0x32 , 0x3a , 0x0a , 0x49 , 0x06 , 0x24 , 0x5c , 0xc2 , 0xd3 , 0xac , 0x62 , 0x91 , 0x95 , 0xe4 , 0x79 ,
0xe7 , 0xc8 , 0x37 , 0x6d , 0x8d , 0xd5 , 0x4e , 0xa9 , 0x6c , 0x56 , 0xf4 , 0xea , 0x65 , 0x7a , 0xae , 0x08 ,
0xba , 0x78 , 0x25 , 0x2e , 0x1c , 0xa6 , 0xb4 , 0xc6 , 0xe8 , 0xdd , 0x74 , 0x1f , 0x4b , 0xbd , 0x8b , 0x8a ,
0x70 , 0x3e , 0xb5 , 0x66 , 0x48 , 0x03 , 0xf6 , 0x0e , 0x61 , 0x35 , 0x57 , 0xb9 , 0x86 , 0xc1 , 0x1d , 0x9e ,
0xe1 , 0xf8 , 0x98 , 0x11 , 0x69 , 0xd9 , 0x8e , 0x94 , 0x9b , 0x1e , 0x87 , 0xe9 , 0xce , 0x55 , 0x28 , 0xdf ,
0x8c , 0xa1 , 0x89 , 0x0d , 0xbf , 0xe6 , 0x42 , 0x68 , 0x41 , 0x99 , 0x2d , 0x0f , 0xb0 , 0x54 , 0xbb , 0x16]
def SM4_SBOX_CALC_WITH_AES(x):
t = G256_new_basis(x, M)
t ^= c1
t = SBOX_AES[t]
t = G256_new_basis(t, L)
t ^= c2
return t
sbox = []
for i in range(256):
sbox.append(SM4_SBOX_CALC_WITH_AES(i)) # 生成sbox
for i,s in enumerate(sbox):
print(f'%02x'%s,', ', end='')
if (i+1)%16==0:
print()
10总结
对 AES 和 SM4 来说,我们都可以把仿射变换和基变换操作的矩阵乘结合起来,简化对应的计算过程,从而减少运算。利用这一思想,我们可以对 AES 和 SM4 的 bit直接进行逻辑运算,避免查表操作。在硬件实现时,可利用该方法构造资源非常受限情况下的S盒实现。在软件上,该方法在抵抗cache攻击方面有效果,同时,我们可以使用bitslice并行技术进行加速。
此外,SM4 的 S 盒可由 AES 表示得出,这一点在 CPU 有 AES 的指令集时,可将 SM4 的 S 盒运算转化为 AES 的 S 盒运算进行加速。
Copyright 2018. Open Security Research, Inc. All rights reserved. 粤ICP备18045701号